Measurement of Neutron-Hidden Neutron Oscillations

Research Overview

This project focused on measuring neutron-hidden neutron oscillations at the Institut Laue-Langevin (ILL), one of the world's leading neutron science facilities. This research represents an exciting frontier in particle physics, exploring potential extensions to the Standard Model through the detection of hidden sectors composed of mirror particles.

Experimental Setup Configuration — Schematic view of the experimental setup showing the cylindrical guide surrounded by the magnetic coil, with the GADGET detector and NANOSC monitor

Theoretical Context

The Mirror Neutron Hypothesis

The hypothesis of neutron-hidden neutron oscillations emerges from theoretical frameworks aiming to explain symmetry breaking in the weak sector (initially proposed by Lee and Yang). This theory postulates parallel sectors hosting mirror copies of all known particles, which could potentially serve as dark matter candidates.

The mixing between ordinary neutrons and hidden neutrons can be represented by a simple Hamiltonian:

\[ H_{nn'} = \begin{pmatrix} E_n & \varepsilon_{nn'} \\ \varepsilon_{nn'} & E_{n'} \end{pmatrix} = \begin{pmatrix} m_n + \Delta E & \varepsilon_{nn'} \\ \varepsilon_{nn'} & m_n + \delta m \end{pmatrix} \]

Where:

$\delta m = m_{n'} - m_n$ represents a small mass difference
$\varepsilon_{nn'} = \tau_{nn'}^{-1}$ is the mixing parameter
$\Delta E$ represents the energy difference that can be experimentally adjusted

Under resonance conditions ( $\Delta E - \delta m = 0$ ), the oscillation probability after a flight time $$t_f$$ is:

\[ P_{nn'}(t_f) = \sin^2(\varepsilon_{nn'} \times t_f) \approx (\varepsilon_{nn'} \times t_f)^2 = (t_f/\tau_{nn'})^2 \]

The experimental approach aims to adjust $\Delta E$ to match $\delta m$ and observe anomalous neutron disappearances that would indicate oscillations.

Experimental Setup

Ultra-Cold Neutron Production

The experiment utilizes ultra-cold neutrons (UCNs), which have sufficiently low energies to be confined by materials and magnetic fields, making them ideal for fundamental physics experiments.

At ILL, the production process involves:

Fast neutrons from fission are slowed in a heavy water moderator
Further cooling occurs in a liquid deuterium moderator at 20K, reaching energies of a few $$\mu$eV$
These cold neutrons are extracted via a curved vertical guide that filters neutrons
A UCN turbine with nickel-coated blades reflects neutrons with a Doppler shift, transforming them into UCNs with energies around $$214$$ neV
These UCNs are then guided to the experiment

UCN Production Process — UCN production process at ILL, from the reactor core to the experimental area

Measurement

The experimental setup consists of:

A cylindrical guide surrounded by a magnetic coil that applies a magnetic field $B$ to the UCNs
This magnetic field eliminates the energy degeneracy of mirror neutrons ( $\Delta E = \mu_n \times B = \delta m$ )
UCNs travel through the guide until they reach the GADGET detector at the end
A monitor (NANOSC detector) is placed upstream of the coil to monitor UCN flux

GADGET Detector — The GADGET detector system showing the ³He and CF₄ gas chambers and photomultiplier tubes

Measurement Protocol — Typical measurement cycle showing the A, B, B, C sequence and corresponding neutron counts

To mitigate effects from long-term flux variations, we implemented a self-normalized measurement sequence dividing each cycle into four 40-second windows with three coil current values scanning magnetic fields:

\[ \{A, B, B, C\} = \{B - 30\text{mA}, B, B, B + 30\text{mA}\} \]

The magnetic field step (30 mA) is chosen to be larger than the resonance. The ratio $R_{ABC}$ between UCN counts at fields B, A, and C is used to identify oscillation presence:

\[ R_{ABC} = \frac{N_B}{\frac{N_A + N_C}{2}} \]

\begin{align*} R_{ABC} &= 1 &&\text{if no oscillation} \\ R_{ABC} &< 1 &&\text{if oscillation at field }B \\ R_{ABC} &> 1 &&\text{if oscillation at field }A\text{ or }C \end{align*}

"Build-up" Effect Analysis

In our experiment, we sequentially shared the UCN flux with another neighboring experiment. As a result, we observed a decrease in neutron flux at the end of each cycle, followed by an increase at the beginning of the next cycle - a phenomenon called "build-up." This non-linear effect, lasting about 30-40 seconds, often extended into the A zone of our measurement sequence.

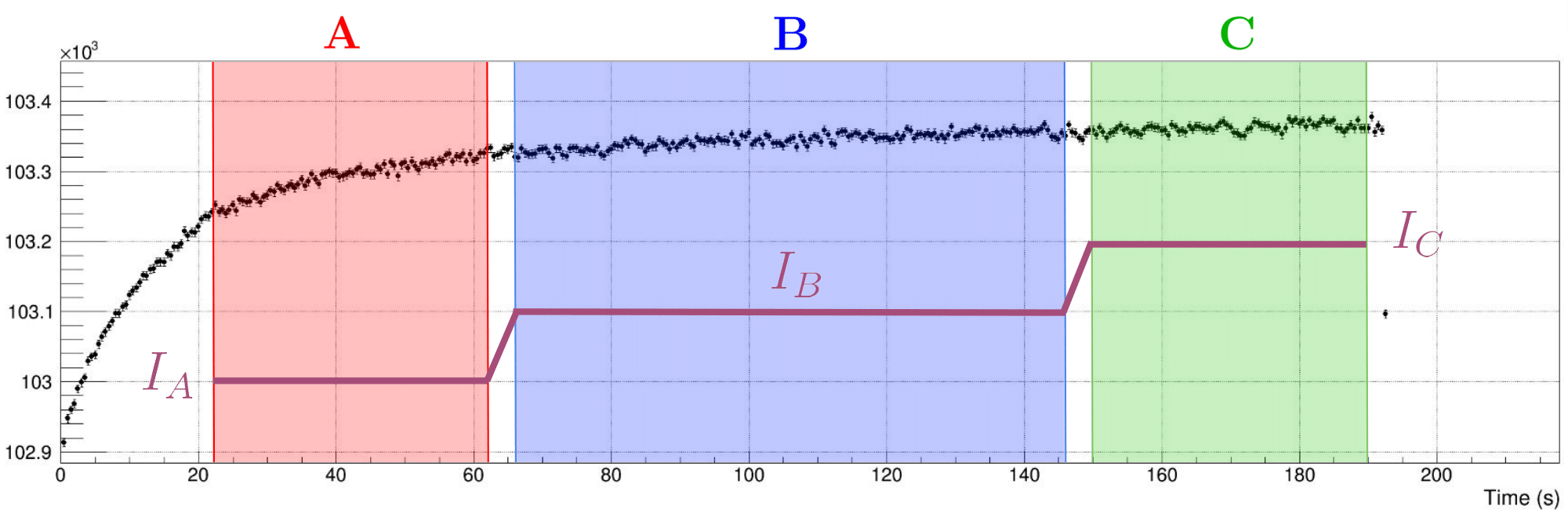
While linear variations in neutron count do not affect our $R_{ABC}$ ratio, non-linear variations can significantly impact it. I therefore studied the effect of cutting out the build-up zone with various cut sizes ( $\Delta t$ ).

R_ABC Distributions — Comparison of R_ABC distributions for different cut values (Δt = 0s vs 10s)

Through careful analysis of $R_{ABC}$ histograms for different $\Delta t$ values (0s vs 10s), I determined that there were no significant variations in $$s$$ with $\Delta t$ .

Turbine Speed Analysis — Analysis of turbine speed variations and their impact on measurement stability

Neutron-Hidden Neutron Oscillation Analysis

Experimental Sensitivity

The primary goal of this experiment (assuming no signal) was to constrain part of the parameter space $\{\delta m, \tau_{nn'}\}$ . Under the resonance hypothesis, I estimated our sensitivity to the parameter $\tau_{nn'}$ at fixed $$B$$ .

Assuming oscillations, we would expect to observe $N_{osc} = N_B \times P_{nn'}(t_f)$ disappearances, where $$N_B$$ is the number of neutrons in zone B used to calculate $R_{ABC}$ . Our sensitivity limit was calculated as:

\[ N_B \times P_{nn'}(t_f) = s \times \sqrt{N_B} \times k \]

Where $$k$$ is the coverage coefficient set to 2 for a 95% confidence level (CL). Therefore:

\[ \tau_{nn'} = t_f \times \sqrt{\frac{\sqrt{N_B}}{s \times k}} \sim \{1.16, 1.39, 1.53, 1.64, 1.74\} \]

Resonance Search

To determine if resonances were present in the experimental $R_{ABC}$ data, I calculated:

\[ \chi^2(B, \tau_{nn'}) = \sum\left[\frac{R^{exp}_{ABC,i} - R^{theo}_{ABC}(B, \tau_{nn'})}{\Delta R_{ABC,i}}\right]^2 \]

Where $R^{theo}_{ABC}(B, \tau_{nn'})$ can be calculated as:

Resonance Search Results — Experimental R_ABC values as a function of magnetic field with null hypothesis fit

\[ R^{theo}_{ABC}(B, \tau_{nn'}) = R^{mean}_{ABC} \times \left(1 - \left(\frac{t_f}{\tau_{nn'}}\right)^2\right) \]

Parameter Exclusions

Based on our analysis, we established a first rough limit:

Parameter Space χ² Analysis — χ² evaluation in the parameter space showing the exclusion curve at 95% CL

\[ \tau_{nn'} > 1.2 \text{ s for } \delta m \in [0.038, 0.287] \text{ neV (95\% CL)} \]

Conclusion and Future Perspectives

This study allowed me to explore regions of the parameter space in the search for neutron-hidden neutron oscillations. The analysis constitutes a first examination of the data and parameter exclusion.

Results Comparison and Future Prospects — Comparison of our experimental results with previous measurements and projected sensitivity for future upgrades. The shaded area represents the excluded parameter space at 95% CL.

The key accomplishments include:

Successfully implementing and validating the measurement protocol
Developing algorithms to analyze build-up effects and turbine speed influences
Establishing a statistically robust approach to parameter exclusion
Setting preliminary constraints on the oscillation parameters

More advanced analyses will be conducted in the future to confirm these results, potentially including deeper studies of magnetic field stability and other systematic effects.

References

Berezhiani, Z. (2009). "More about neutron–mirror neutron oscillation". Eur. Phys. J. C 64, 421–431.
Saenz, W. (2022). "Neutron to Hidden Neutron Oscillations in Ultra-Cold Neutron Beams". PhD thesis. Normandie Université.

Gaby BRENOT